Rozwiązywanie nieliniowych statycznych problemów elementów skończonych

1. System sprężynowy przymocowany do sztywnej ściany
2. Dlaczego rozwiązanie nieliniowego problemu nie może się zbiegać
3. Przypadek 1: Wstępne podejście zbyt daleko od decyzji
4. Przypadek 2: zadanie nie ma rozwiązania
5. Przypadek 3: Problem nie jest gładki i niezróżnicowany
6. Interpretacja pliku dziennika COMSOL
7. Wyjaśnienia

Tutaj zaczynamy przegląd algorytmów używanych do rozwiązywania nieliniowych statycznych problemów z elementami skończonymi. Ten materiał jest zademonstrowany na przykładzie bardzo prostego zadania 1D i opiera się na poprzednim artykule. Rozwiązanie liniowych modeli statycznych elementów skończonych .

System sprężynowy przymocowany do sztywnej ściany

Rozważmy system przedstawiony poniżej: sprężyna jest przymocowana na jednym końcu do sztywnej ściany, a do jej drugiego końca przyłożona jest pewna siła. Sztywność sprężyny jest funkcją odległości, na której się rozciąga k (u) = exp (u). Oznacza to, że sztywność sprężyny wzrasta wykładniczo po rozciągnięciu.

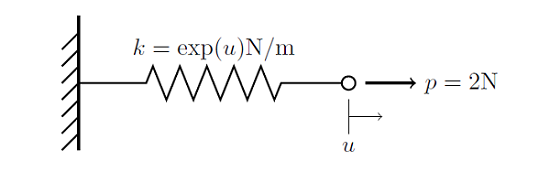
Chcemy znaleźć przesunięcie końca sprężyny w miejscu przyłożenia siły. Tak jak wcześniej problem liniowy , możemy napisać funkcję opisującą równowagę sił w węźle dla nieliniowego problemu elementów skończonych:

f (u) = pk (u) u = p-exp (u) u

W konkretnym przypadku tylko sztywność sprężyny zależy od przemieszczenia, ale w bardziej ogólnym przypadku zarówno zastosowane obciążenie, jak i właściwości elementów mogą arbitralnie zależeć od rozwiązania problemu nieliniowego.

Narysujmy wykres tej funkcji, pamiętając, że próbujemy znaleźć u takie, że f (u) = 0.

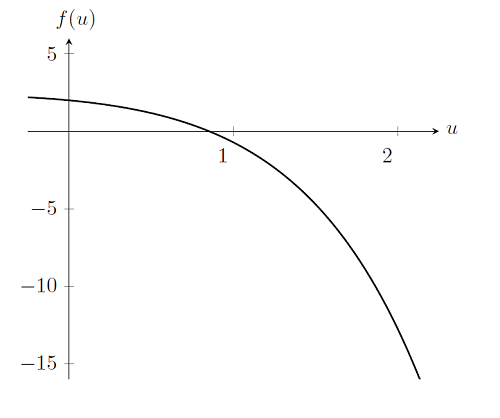
Znalezienie rozwiązania problemu w rzeczywistości różni się tylko nieznacznie od przypadku liniowego. Przypomnijmy, że aby rozwiązać problem liniowy, wykonaliśmy pojedynczą iterację Newtona-Raphsona - i robimy dokładnie to samo tutaj:

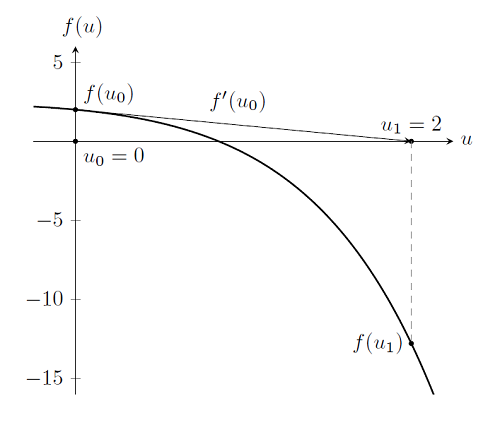
Jak widać, ponownie zaczynamy od początkowego przybliżenia u_0 = 0 i oceniamy funkcję, f (u_0) i jej pochodną, ​​f '(u_0). Daje nam to punkt u_1. Sprawdzając, widzimy, że ten punkt nie jest rozwiązaniem, ponieważ f (u_1) ne 0. Ale jeśli będziemy kontynuować iterację Newtona-Raphsona, jak pokazano poniżej, staje się oczywiste, że zbliżamy się do rozwiązania problemu. (Aby uzyskać bardziej szczegółowe badanie tego algorytmu, możesz użyć tego łącza Metoda Newtona .)

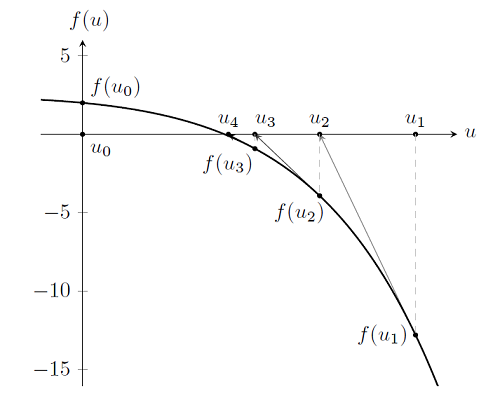
Stąd znalezienie rozwiązania problemu nieliniowego jest zasadniczo identyczne z rozwiązaniem problemu liniowego, z wyjątkiem faktu, że teraz podejmujemy wiele kolejnych kroków Newtona-Raphsona, aby uzyskać rozwiązanie. W rzeczywistości możemy nadal wykonywać iteracje i przychodzić jak najbliżej rozwiązania, ale nie jest to konieczne. Jak wspomniano wcześniej, prędzej czy później osiągniemy komputerową dokładność przedstawiania liczb na komputerze, więc zawsze istnieje praktyczna granica tego, jak blisko można dojść do rozwiązania. Spójrzmy na wyniki kilku iteracji:

i u_i | f (u_i) | | u_ {i-1} -u_i | | f (u_ {i-1}) - f (u_i) | 0 0.000 2.000 1 2.000 12.77 2.000 10.77 2 1.424 3.915 0.576 8.855 3 1.035 0.914 0.389 3.001 4 0.876 0.104 0.159 0.810 5 0.853 0.002 0.0023 0.102 6 0.852 0.001 0.001 0.001

Widzimy, że po sześciu iteracjach różnica między dwiema kolejnymi wartościami f (u) i u, jak również wartość bezwzględna f (u), zmniejszyła się do 0,001 lub mniej. Po sześciu iteracjach w Newton-Raphson, zaczynając od u_0 = 0, rozwiązanie zbiegło się z błędem mniejszym niż 0,001. Podczas rozwiązywania problemów nieliniowych stosujemy ten algorytm, aż rozwiązanie zbiegnie się z pożądaną dokładnością. Istnieje również drugie kryterium zakończenia: solver musi wykonać nie więcej niż pewną liczbę iteracji. Niezależnie od tego, które kryterium jest spełnione, najpierw - błąd względny lub liczba iteracji - solver zatrzyma proces. Należy również pamiętać o problemie skalowania numerycznego, który omówiliśmy w artykule na blogu dotyczącym rozwiązywania problemów ze statycznymi liniowymi elementami skończonymi. Kryterium błędu względnego dotyczy skalowanego, a nie bezwzględnego wektora rozwiązania.

Chociaż jest to znacznie trudniejsze do pokazania, algorytm używany do rozwiązywania problemów nieliniowych, w przypadku gdy u jest wektorem, pozostaje taki sam jak w przypadku zwykłego problemu. Jednakże, rozwiązując problem z setkami, tysiącami, a nawet milionami stopni swobody, pożądane jest, aby liczba iteracji Newtona-Raphsona była jak najmniejsza. Przypomnij sobie, że musimy rozwiązać problem MathBf {u} _ {i + 1} = Mathbf {u} _ {i} - [Mathbf {f} '(Mathbf {u} _ {i})] ^ { -1} matembf {f} (Mathbf {u} _ {i}), w którym obliczanie odwrotnych pochodnych jest procedurą najbardziej zasobochłonną. Aby uniknąć obliczeń w zakresie wartości, które oczywiście nie zawierają rozwiązania, i zminimalizować liczbę iteracji Newtona-Raphsona, środowisko COMSOL wykorzystuje współczynnik relaksacji (współczynnik relaksacji) . Spójrzmy jeszcze raz na początkową iterację Newtona-Raphsona i jej wykres, i zanotuj to dla niej | MathBf {f} (MathBf {u} _ {i + 1}) |> | MathBf {F} (Mathbf {u } _ {i}) | . Więc dla tej iteracji robimy duży krok. Gdy tak się stanie, COMSOL przeszukuje interwał [matematyczne {u} _ {i}, matematyczne {u} _ {i + 1}] punktu matematyczne {u} _ {tłumione} = matematyczne {u} _i + alpha (matematyczne {u} _ {i + 1} - matematyczne {u} _i) takie, że | matematyczne {f (u} _ {tłumione}) | <| matematyczne {f (u} _ {i }) | . Następnie wznawia się schemat iteracji Newtona-Raphsona.

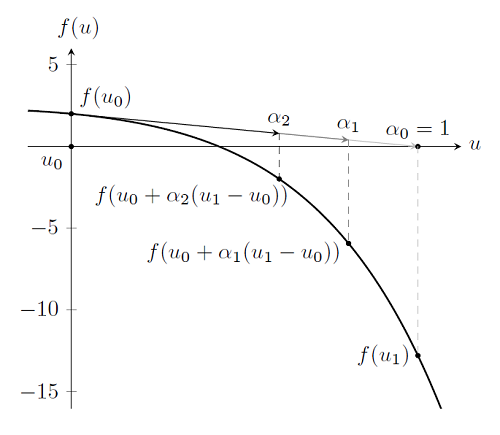
Parametr alfa jest znany jako współczynnik relaksacji (współczynnik relaksacji) i zmienia się w przedziale 0 <alfa 1. Przy alfa w prawo 0 mówimy, że relaksacja wzrasta , a alfa = 1 oznacza, że ​​zadanie nie jest zrelaksowane. Ta metoda jest dość atrakcyjna, ponieważ wymaga od środowiska COMSOL tylko oszacowania wartości MathBf {f (u} _ {damped}), a koszty obliczeniowe są znacznie niższe niż obliczenia pochodnych matematyki {f '(u} _ {i}) i odwrotność wartości [Mathbf {f} '(Mathbf {u} _i)] ^ Mathbf {-1}.

Należy podkreślić, że parametr relaksacji nie ma bezpośredniej interpretacji fizycznej. Chociaż metoda ta bardzo dobrze poprawia konwergencję, współczynnik relaksacji nie ma żadnego fizycznego znaczenia. Co więcej, chociaż środowisko COMSOL pozwala na ręczne dostosowanie współczynnika relaksacji, nie ma żadnych fizycznych wymagań wstępnych ani reprezentacji modelu, jak i kiedy to robić. Domyślny algorytm wygładzania jest bardzo trudny do pokonania przy ręcznej regulacji. Istnieją jednak inne metody, powodowane z reguły przez fizykę problemu, które działają dobrze w przypadkach, gdy metoda relaksacji Newtona-Raphsona zbiega się powoli lub wcale nie zbiega się.

Dlaczego rozwiązanie nieliniowego problemu nie może się zbiegać

Problemy nieliniowe są z natury trudne do rozwiązania, ponieważ istnieje wiele powodów, dla których procedura rozwiązania omówiona powyżej może nie być zbieżna. Chociaż istnieje wiele powodów metoda Newtona-Raphsona może się nie udać (metoda Newtona-Raphsona zawodzi) , ograniczamy się do omówienia następujących praktycznych przypadków.

Przypadek 1: Wstępne podejście zbyt daleko od decyzji

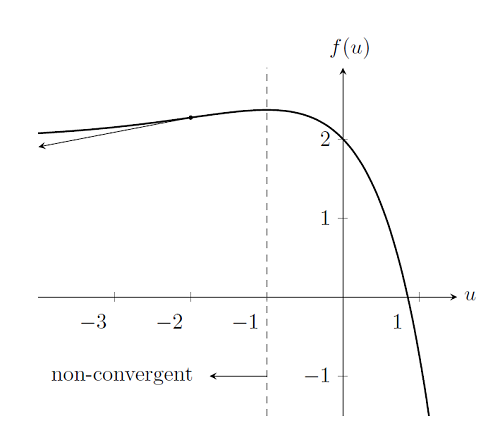
Przede wszystkim rozważamy ten sam nieliniowy problem, ale z inną pozycją początkową, na przykład u_0 = -2. Jak widać na poniższym wykresie, jeśli wybierzemy punkt początkowy w regionie u_0 le-1, metoda Newtona-Raphsona nie może znaleźć rozwiązania, ponieważ pochodne f (u) nie dają punktu przecięcia zbliżającego się do rozwiązania. Rozwiązania nie można znaleźć po lewej stronie u_0 = -1, więc te punkty początkowe znajdują się poza promieniem zbieżności metody Newtona-Raphsona. To znaczy Ze względu na wybór wstępnego przybliżenia metoda Newtona-Raphsona może nie być zbieżna, nawet jeśli istnieje rozwiązanie . Zatem, w przeciwieństwie do przypadku liniowego, gdy prawidłowo postawiony problem będzie zawsze rozwiązywany, zbieżność modeli nieliniowych silnie zależy od wyboru pozycji początkowej. Później powrócimy do pytania, jak najlepiej wybrać wstępne przybliżenie.

Przypadek 2: zadanie nie ma rozwiązania

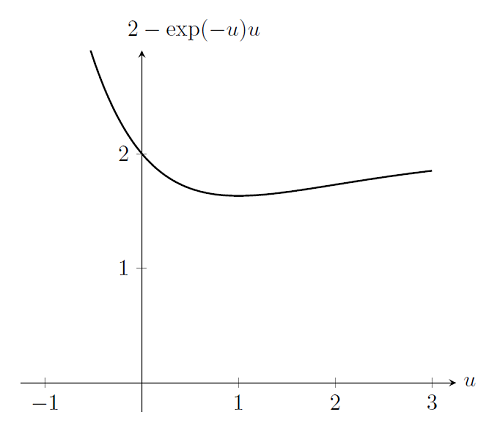
Nieliniowy solver również zawiedzie, jeśli sam problem nie ma rozwiązania. Powróćmy ponownie do problemu rozważanego powyżej, ale ze sztywnością sprężyny k (u) = exp (-u). Innymi słowy, przy rozciągnięciu zmniejsza się sztywność sprężyny. Jeśli zbudujemy wykres f (u) dla obciążenia p = 2, zobaczymy, że rozwiązanie nie istnieje. Niestety, algorytm Newtona-Raphsona nie może sam tego określić; algorytm po prostu spróbuje znaleźć rozwiązanie i zakończyć pracę po zdefiniowanej przez użytkownika liczbie iteracji.

Przypadek 3: Problem nie jest gładki i niezróżnicowany

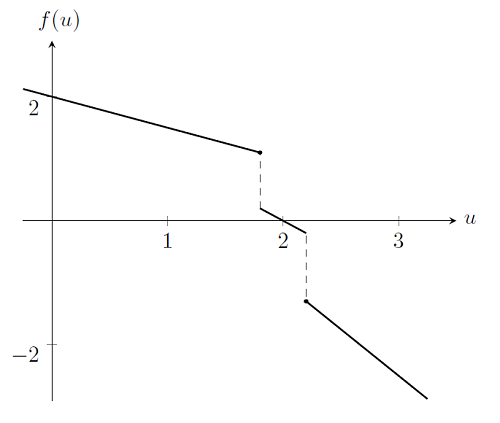
Wreszcie rozważamy przypadek, w którym właściwości materiału zmieniają się w sposób podobny do skoku. Na przykład rozważmy ten sam system, co poprzednio, ale przy sztywności sprężyny przyjmującej różne wartości w różnych zakresach rozciągania, wartość k = 0,5 dla u1.8, wartość k = 1 dla 1,8 <u <2,2, a k = 1.5 dla u2.2. Jeśli skonstruujemy wykres f (u) dla tego przypadku, zobaczymy, że jest on niezróżnicowany i przerwany, a to narusza wymagania metody Newtona-Raphsona. Łatwo zauważyć poprzez bezpośrednią weryfikację, że jeśli punkt początkowy nie zostanie wybrany w przedziale 1,8 <u <2,2, to iteracje Newtona-Raphsona będą oscylować poza tym zakresem.

Podsumowując: opisaliśmy metodę relaksacji Newtona-Raphsona używaną do rozwiązywania nieliniowych problemów z elementami skończonymi i omówiliśmy kryteria ich zbieżności. Wymieniliśmy kilka powodów, dla których ta metoda może się nie udać, próbując znaleźć rozwiązanie, w tym:

• Wstępne przybliżenie wybrane zbyt daleko od rozwiązania
• Ustawiono zadanie, które nie ma rozwiązania.
• Zadanie nie jest gładkie i nieróżnialne.

Interpretacja pliku dziennika COMSOL

Plik dziennika (dziennik systemu)

W niedalekiej przyszłości omówimy sposoby rozwiązania wszystkich tych problemów, ale najpierw spójrzmy na plik dziennika typowego nieliniowego problemu elementów skończonych. Spójrz na poniższy tekst pliku dziennika (uzupełniony numerami linii) geometrycznego nieliniowego problemu z mechaniki strukturalnej:

1) Stacjonarny Solver 1 w Solver 1 rozpoczął się 10 lipca 2013 r. 15:23:07. 2) Rozwiązania nieliniowe 3) Liczba stopni swobody rozwiązana dla: 2002. 4) Znaleziono symetryczne macierze. 5) Skale zmiennych zależnych: 6) Pole przemieszczenia (Materiał) (mod1.u): 1 7) Iter ErrEst Damping Stepsize #Res #Jac #Sol 8) 1 6,1 0,1112155 7 3 1 3 9) 2 0,12 0,6051934 1,2 4 2 5 10) 3 0,045 1,0000000 0,18 5 3 7 11) 4 0,012 1,0000000 0,075 6 4 9 12) 5 0,0012 1,0000000 0,018 7 5 11 13) 6 1,6e-005 1,0000000 0,0015 8 6 13 14) Stacjonarny solver 1 w Solver 1: Rozwiązanie czas: 1 s 15) Pamięć fizyczna: 849 MB 16) Pamięć wirtualna: 946 MB

Wyjaśnienia

• Linia 1 podaje typ wywoływanego solwera (kalkulator) i czas rozpoczęcia zadania.
• Linia 2 podaje, że wywołane oprogramowanie jest nieliniowym rozwiązaniem systemu.
• Linia 3 podaje rozmiar problemu pod względem liczby stopni swobody.
• Linia 4 podaje typ macierzy elementów skończonych.
• Linie 5-6 opcje skalowania raportu. W tym przypadku skala pola przemieszczenia wynosi 1 m, co jest odpowiednią wartością dla oczekiwanej wartości rozwiązania.
• Linie 7-13 informują, że sześć iteracji Newtona-Raphsona było wymaganych do uzyskania rozwiązania zbieżnego. Pierwsza kolumna podaje numer iteracji, a druga zawiera informacje o błędzie użytym do określenia zbieżności rozwiązania. Domyślnie kryterium zbieżności wynosi 0,001. Trzecia kolumna pokazuje, że relaksację zastosowano w dwóch pierwszych iteracjach, ale kroki 3-6 pozostały niezauważone.
• Linie 14–16 informują o czasie otrzymania rozwiązania i wymaganiach dotyczących pamięci.

Teraz zrozumiałeś, w jaki sposób nieliniowe problemy statyczne są rozwiązywane w środowisku COMSOL, a także wiedzę na temat interpretowania rekordów w pliku dziennika.