Рашэння нелінейных статычных Задач Канчатковых Элементаў

1. Сістэма спружыны, прымацаванай да жорсткай сцяны
2. Чаму рашэння нелінейных Задачы Можа не сысці
3. Выпадак 1: Пачатковае Набліжэнне Занадта Далёка ад Рашэнні
4. Выпадак 2: Задача Ня Ці мае Рашэнні
5. Выпадак 3: Задача Ня Гладкая і Недифференцируемая
6. Інтэрпрэтацыя Log-Файла асяроддзя COMSOL
7. тлумачэнні

Тут мы пачынаем агляд алгарытмаў выкарыстоўваюцца для вырашэння нелінейных статычных вядома-элементных задач. Гэты матэрыял дэманструецца на прыкладзе вельмі просты 1D задачы і грунтуецца на папярэдняй артыкуле Рашэнне лінейна статычныя Мадэляў Канчатковых Элементаў .

Сістэма спружыны, прымацаванай да жорсткай сцяны

Разгледзім сістэму, паказаную ніжэй: спружына адным канцом замацаваная на жорсткай сценцы, а да іншага яе канца прыкладзеная некаторая сіла. Жорсткасць спружыны ёсць функцыя адлегласці, на якое яна расцягваецца k (u) = exp (u). Гэта значыць жорсткасць спружыны павялічваецца экспанентна пры расцяжэнні.

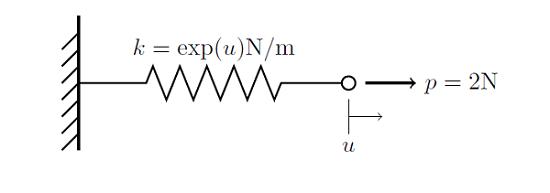
Мы хочам знайсці зрушэнне канца спружыны ў месцы прыкладання сілы. Гэтак жа сама як мы рабілі раней для лінейнай задачы , Мы можам запісаць функцыю якая апісвае баланс сіл у вузле для нелінейнай задачы канчатковых элементаў:

f (u) = pk (u) u = p-exp (u) u

У канкрэтным выпадку, толькі жорсткасць спружыны залежыць ад зрушэння, але ў больш агульным выпадку, і прыкладваюць нагрузка, і ўласцівасці элементаў, могуць адвольным чынам залежаць ад рашэння нелінейнай задачы.

Намалюем графік гэтай функцыі, маючы на ​​ўвазе, што мы спрабуем знайсці u такое, што f (u) = 0.

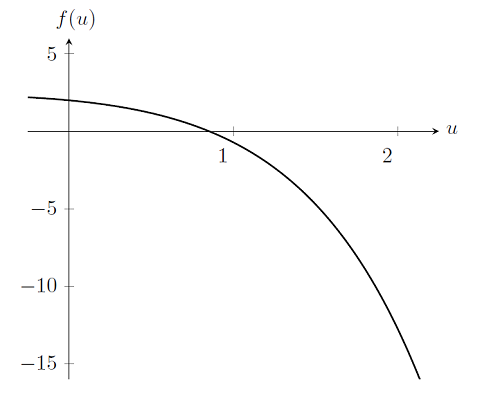
Знаходжанне рашэння задачы, у рэчаіснасці, толькі нязначна адрозніваецца ад лінейнага выпадку. Успомнім, што для таго каб вырашыць лінейную задачу, мы рабілі адзіночную ітэрацыю па Ньютану-Рафсону - і робім дакладна тое ж самае тут:

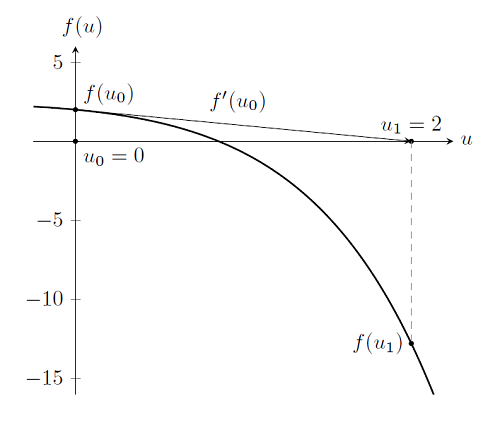
Як можна заўважыць, мы зноў стартуем з пачатковага набліжэння u_0 = 0, і ацэньваем функцыю, f (u_0), і яе вытворную, f '(u_0). Гэта дае нам кропку u_1. Правяраючы, мы пераконваемся, што гэтая кропка не з'яўляецца рашэннем, так як f (u_1) \ ne 0. Але калі мы будзем працягваць рабіць ітэрацыі па Ньютану-Рафсону, як паказана ніжэй, то становіцца відавочным, што мы набліжаемся да вырашэння задачы. (Для больш падрабязнага вывучэння гэтага алгарытму, вы можаце выкарыстоўваць гэтую спасылку метад Ньютана .)

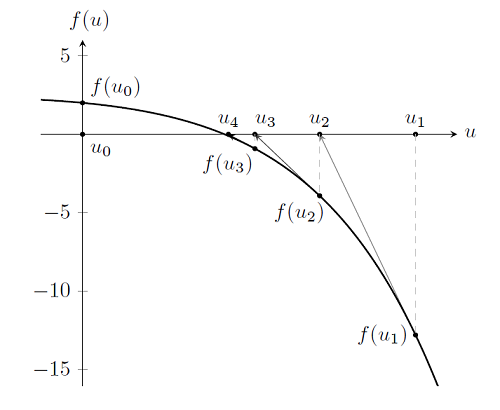
Такім чынам, знаходжанне рашэння нелінейнай задачы па сутнасці ідэнтычна рашэнню лінейнай задачы, за выключэннем таго, што зараз мы робім шматразовыя паслядоўныя крокі па Ньютану-Рафсону, каб атрымаць рашэнне. На самай справе, мы можам працягваць рабіць ітэрацыі і калі заўгодна блізка падысці да вырашэння, але ў гэтым няма неабходнасці. Як абмяркоўвалася раней, рана ці позна мы дасягнем машыннай дакладнасці прадстаўлення лікаў на кампутары, так што заўсёды ёсць практычны мяжа наколькі можна наблізіцца да вырашэння. Давайце паглядзім на вынікі некалькіх ітэрацый:

i u_i | f (u_i) | | U_ {i-1} -u_i | | F (u_ {i-1}) - f (u_i) | 0 0.000 2.000 1 2.000 12.77 2.000 10.77 2 1.424 3.915 0.576 8.855 3 1.035 0.914 0.389 3.001 4 0.876 0.104 0.159 0.810 5 0.853 0.002 0.023 0.102 6 0.852 0.001 0.001 0.001

Мы бачым, што пасля шасці ітэрацый розніца паміж двума паслядоўнымі значэннямі f (u), і u, а таксама абсалютная значэнне f (u), паменшылася да 0.001 або менш. Пасля шасці ітэрацый па Ньютану-Рафсону пачынаючы з u_0 = 0, рашэнне сышлося з хібнасцю менш 0.001. Пры вырашэнні нелінейных задач, мы ўжываем гэты алгарытм да таго часу, пакуль рашэнне не сыдзецца з жаданай дакладнасцю. Маецца і другі крытэрый для завяршэння: решатель павінен зрабіць не больш за пэўнай колькасці ітэрацый. Па-за залежнасці ад таго, які крытэрый выканаецца першым - адносная хібнасць альбо лічбу ітэрацый - решатель спыніць працэс. Таксама, неабходна памятаць аб праблеме колькаснага маштабавання, якую мы абмяркоўвалі ў артыкуле блога аб рашэнні лінейных статычных вядома-элементных задач. Крытэрый адноснай хібнасці прымяняецца да маштабавацца, а не да абсалютнага вектару рашэння.

Хоць паказаць гэта значна складаней, але алгарытм які выкарыстоўваецца для вырашэння нелінейных задач, у выпадку калі u з'яўляецца вектарам застаецца тым жа, што і для звычайнай задачы. Аднак, пры рашэнні задачы з сотнямі, тысячамі або, нават, з мільёнамі ступеняў свабоды, пажадана, каб колькасць ітэрацый Ньютана-Рафсона было мінімальна магчымым. Нагадаем, што нам неабходна вырашыць задачу \ mathbf {u} _ {i + 1} = \ mathbf {u} _ {i} - [\ mathbf {f} '(\ mathbf {u} _ {i})] ^ { -1} \ mathbf {f} (\ mathbf {u} _ {i}), у якой вылічэнне зваротных вытворных з'яўляецца найбольш ресурсозатратной працэдурай. Каб пазбегнуць вылічэнняў у галіне значэнняў, загадзя не змяшчаюць рашэнні, і мінімізаваць лік ітэрацый Ньютана-Рафсона, у асяроддзі COMSOL выкарыстоўваецца релаксацыйны множнік (каэфіцыент рэлаксацыі). Паглядзім зноў на пачатковую ітэрацыю Ньютана-Рафсона і яе графік, і заўважым, што для яе | \ mathbf {f} (\ mathbf {u} _ {i + 1}) |> | \ mathbf {f} (\ mathbf {u } _ {i}) | . Так што для гэтай ітэрацыі, мы робім занадта вялікі крок. Калі гэта адбываецца, COMSOL ажыццяўляе пошук ўздоўж інтэрвалу [\ mathbf {u} _ {i}, \ mathbf {u} _ {i + 1}] пункту \ mathbf {u} _ {damped} = \ mathbf {u} _i + \ alpha (\ mathbf {u} _ {i + 1} - \ mathbf {u} _i) такой, што | \ mathbf {f (u} _ {damped}) | <| \ mathbf {f (u} _ {i }) | . Пасля чаго, схема ітэрацый Ньютана-Рафсона аднаўляецца з гэтай кропкі.

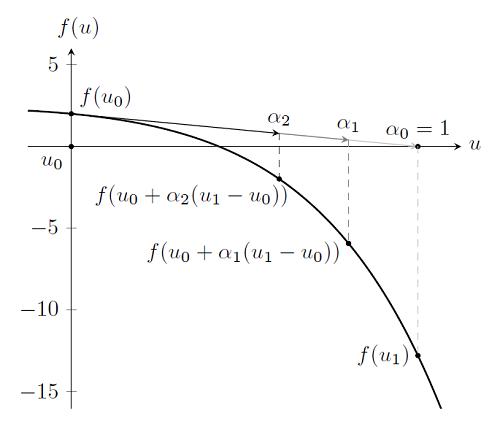
Параметр \ alpha вядомы, як релаксацыйны множнік (каэфіцыент рэлаксацыі) і змяняецца ў інтэрвале 0 <\ alpha \ le 1. Пры \ alpha \ rightarrow 0 мы кажам, што рэлаксацыя ўзрастае, а \ alpha = 1 значыць, што задача не срелаксирована. Гэты метад досыць прывабны, бо патрабуе ад асяроддзя COMSOL толькі ацэнкі значэння \ mathbf {f (u} _ {damped}), і вылічальныя затраты пры гэтым значна ніжэй, чым вылічэнне вытворных \ mathbf {f '(u} _ {i}) і зваротных да іх велічынь [\ mathbf {f} '(\ mathbf {u} _i)] ^ \ mathbf {-1}.

Важна падкрэсліць, што параметр рэлаксацыі не мае непасрэднай фізічнай інтэрпрэтацыі. Хоць метад вельмі добра паляпшае збежнасць, ніякага фізічнага сэнсу релаксацыйны множнік не нясе. Больш за тое, хаця сярод COMSOL дазваляе ўручную рэгуляваць релаксацыйны множнік, няма ніякіх фізічных перадумоў або мадэльных уяўленняў, як і калі варта гэта рабіць. Абраны па змаўчанні алгарытм згладжвання, вельмі цяжка перасягнуць з дапамогай ручной рэгулявання. Аднак, існуюць іншыя метады, абумоўленыя, як правіла, фізікай задачы, якія добра працуюць у тых выпадках, калі релаксацыйны метад Ньютана-Рафсона сыходзіцца павольна ці ўвогуле не сыходзіцца.

Чаму рашэння нелінейных Задачы Можа не сысці

Нелінейныя задачы па сваёй сутнасці складана вырашыць, паколькі існуе мноства прычын, з-за якіх разгледжаная вышэй працэдура рашэння можа не сысціся. Хоць маецца шмат прычын, па якіх the Newton-Raphson method can fail (метад Ньютана-Рафсона трывае няўдачу) , Мы абмяжуемся абмеркаваннем наступных практычных выпадкаў.

Выпадак 1: Пачатковае Набліжэнне Занадта Далёка ад Рашэнні

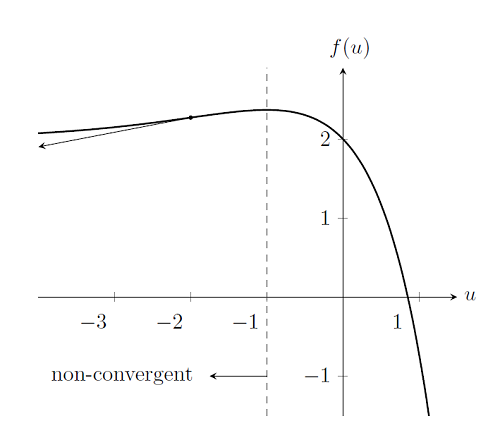
Перш за ўсё, разгледзім тую ж самую нелінейную задачу, але з іншага стартавай пазіцыяй, напрыклад, u_0 = -2. Як можна заўважыць з графіка ніжэй, калі мы абярэм пачатковую кропку ў галіне u_0 \ le-1, метад Ньютана-Рафсона не зможа знайсці рашэнне, так як вытворныя f (u) не даюць кропкі скрыжавання, надыходзячай да вырашэння. Рашэнне не можа быць знойдзена злева ад u_0 = -1, так што гэтыя пачатковыя кропкі знаходзяцца па-за радыуса збежнасці метаду Ньютана-Рафсона. Г.зн. з-за выбару пачатковага набліжэння метад Ньютана-Рафсона можа не сысціся, нават калі рашэнне існуе. Такім чынам, у адрозненне ад лінейнага выпадку, калі карэктна пастаўленая задача заўсёды будзе вырашана, збежнасць нелінейных мадэляў у моцнай ступені залежыць ад выбару стартавай пазіцыі. Пазней мы вернемся да пытання, як найлепшым спосабам выбраць пачатковую набліжэнне.

Выпадак 2: Задача Ня Ці мае Рашэнні

Нелінейны решатель таксама пацерпіць няўдачу, калі задача сама па сабе не мае рашэння. Вернемся зноў да задачы, разгледжанай вышэй, але з калянасцю спружыны k (u) = \ exp (-u). Іншым словамі, з расцяжэннем жорсткасць спружыны памяншаецца. Калі мы пабудуем графік f (u) для нагрузкі p = 2, мы ўбачым, што рашэнне не існуе. Да няшчасця, алгарытм Ньютана-Рафсона не можа вызначыць гэта самастойна; алгарытм проста будзе спрабаваць знайсці рашэнне і завершыць сваю працу пасля зададзенага карыстальнікам колькасці ітэрацый.

Выпадак 3: Задача Ня Гладкая і Недифференцируемая

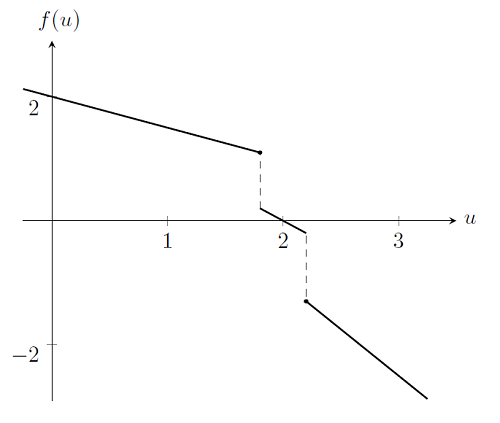
Нарэшце, разгледзім выпадак, калі ўласцівасці матэрыялу змяняюцца скачкападобнай чынам. Напрыклад, разгледзім такую ​​ж сістэму, як і перад гэтым, але з калянасцю спружыны, якая прымае розныя значэнні ў розных дыяпазонах расцяжэнняў, значэнне k = 0.5 для u \ le1.8, значэнне k = 1 для 1.8 <u <2.2, і k = 1.5 для u \ ge2.2. Калі мы пабудуем графік f (u) для гэтага выпадку, мы ўбачым, што ён недифференцируем і разрыву, а гэта парушае патрабаванні метаду Ньютана-Рафсона. Лёгка пераканацца непасрэднай праверкай, што калі стартавая кропка абраная не ў інтэрвале 1.8 <u <2.2, то ітэрацыі Ньютана-Рафсона будуць осциллировать за межамі гэтага дыяпазону.

Падвядзем вынікі: мы апісалі релаксацыйны метад Ньютана-Рафсона, які выкарыстоўваецца для вырашэння нелінейных вядома-элементных задач і абмеркавалі крытэрыі яго збежнасці. Мы паказалі некалькі прычын, па якіх гэты метад можа пацярпець няўдачу пры спробе знайсці рашэнне, уключаючы:

• Пачатковае набліжэнне абрана занадта далёка ад рашэння
• Пастаўлена задача, якая не мае рашэнні
• Задача негладкой і недифференцируемая

Інтэрпрэтацыя Log-Файла асяроддзя COMSOL

Log-файл (сістэмны часопіс)

У бліжэйшы час мы абмяркуем шляху вырашэння ўсіх гэтых пытанняў, але перш, давайце паглядзім на log-файл тыповай нелінейнай задачы канчатковых элементаў. Паглядзіце на прыведзены ніжэй тэкст log-файла (дапоўненага нумарамі радкоў) геаметрычнай нелінейнай задачы з будаўнічай механікі:

1) Stationary Solver 1 in Solver 1 started at 10-Jul-2013 15:23:07. 2) Nonlinear solver 3) Number of degrees of freedom solved for: 2002. 4) Symmetric matrices found. 5) Scales for dependent variables: 6) Displacement field (Material) (mod1.u): 1 7) Iter ErrEst Damping Stepsize #Res #Jac #Sol 8) 1 6.1 0.1112155 7 3 1 3 9) 2 0.12 0.6051934 1.2 4 2 5 10) 3 0.045 1.0000000 0.18 5 3 7 11) 4 0.012 1.0000000 0.075 6 4 9 12) 5 0.0012 1.0000000 0.018 7 5 11 13) 6 1.6e-005 1.0000000 0.0015 8 6 13 14) Stationary Solver 1 in Solver 1: Solution time: 1 s 15) Physical memory: 849 MB 16) Virtual memory: 946 MB

тлумачэнні

• Радок 1 паведамляе пра тып выкліканага решателя (вылічальніка) і часу пачатку выканання задачы.
• Радок 2 паведамляе, што выкліканае праграмнае забеспячэнне - гэта решатель нелінейных сістэм.
• Радок 3 паведамляе аб памеры задачы ў тэрмінах ліку ступеняў волі.
• Радок 4 паведамляе пра тып матрыцы канчатковых элементаў.
• Радкі 5-6 паведамляюць пра параметры маштабавання. У дадзеным выпадку маштаб поля зрушэння ёсць 1 м, што з'яўляецца прыдатным значэннем для чаканай велічыні рашэння.
• Радкі 7-13 паведамляюць, што шэсць ітэрацый па Ньютану-Рафсону спатрэбілася для атрымання збежных рашэння. Першы слупок паведамляе аб нумары ітэрацыі, а ў другім прыведзены звесткі пра памылку, якія выкарыстоўваюцца для вызначэння збежнасці рашэння. Па змаўчанні, крытэрый збежнасці роўны 0.001. Трэцяя калонка паказвае, што для першых двух ітэрацый выкарыстоўвалася рэлаксацыя, але крокі 3-6 засталіся не срелаксированными.
• Радкі 14-16 паведамляюць пра час атрымання рашэння і патрабаваннях да аб'ёму памяці.

Цяпер вы набылі разуменне таго, як вырашаюцца нелінейныя статычныя задачы ў асяроддзі COMSOL, а таксама веды, як інтэрпрэтаваць запісы ў log-файле.