- Система пружини, прикріпленою до жорсткої стіні
- Чому Рішення Нелінійної Завдання Можуть Не Зійтися
- Випадок 1: Початкове Наближення Занадто Далеко від Рішення
- Випадок 2: Завдання Чи не має Рішення
- Випадок 3: Завдання Чи не Гладка і недіфференціруемого
- Інтерпретація Log-файлу середовища COMSOL
- роз'яснення
Тут ми починаємо огляд алгоритмів використовуваних для вирішення нелінійних статичних кінцево-елементних завдань. Цей матеріал демонструється на прикладі дуже простий 1D завдання і грунтується на попередній статті Рішення лінійних статичних Моделей Кінцевих Елементів .
Система пружини, прикріпленою до жорсткої стіні
Розглянемо систему, показану нижче: пружина одним кінцем закріплена на жорсткій стінці, а до іншого її кінця прикладена деяка сила. Жорсткість пружини є функція відстані, на яке вона розтягується k (u) = exp (u). Тобто жорсткість пружини збільшується експоненціально при розтягуванні.
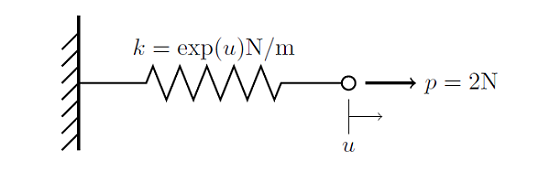
Ми хочемо знайти зміщення кінця пружини в місці прикладання сили. Точно також як ми робили раніше для лінійної задачі , Ми можемо записати функцію описує баланс сил в вузлі для нелінійної задачі кінцевих елементів:
f (u) = pk (u) u = p-exp (u) u
У конкретному випадку, тільки жорсткість пружини залежить від зсуву, але в більш загальному випадку, і прикладається навантаження, і властивості елементів, можуть довільним чином залежати від рішення нелінійної задачі.
Намалюємо графік цієї функції, маючи на увазі, що ми намагаємося знайти u таке, що f (u) = 0.
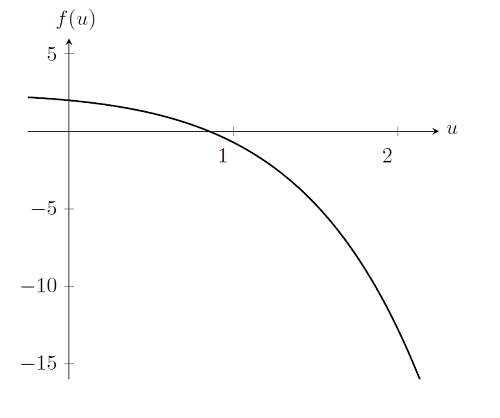
Знаходження рішення задачі, в дійсності, лише трохи відрізняється від лінійного випадку. Згадаймо, що для того щоб вирішити лінійну задачу, ми робили одиночну ітерацію по Ньютону-Рафсона - і робимо точно те ж саме тут:
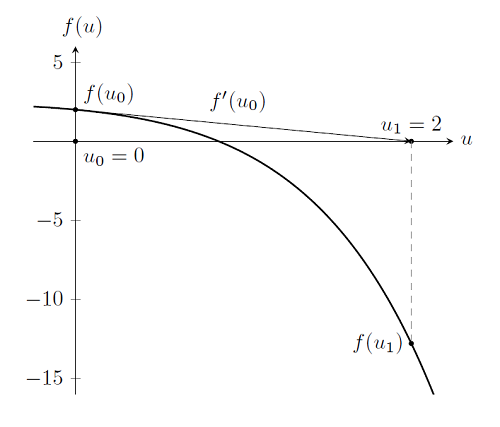
Як можна помітити, ми знову стартуємо з початкового наближення u_0 = 0, і оцінюємо функцію, f (u_0), і її похідну, f '(u_0). Це дає нам точку u_1. Перевіряючи, ми переконуємося, що ця точка не є рішенням, так як f (u_1) \ ne 0. Але якщо ми продовжимо робити ітерації по Ньютону-Рафсона, як показано нижче, то стає очевидним, що ми наближаємося до вирішення завдання. (Для більш детального вивчення цього алгоритму, ви можете використовувати цю посилання метод Ньютона .)
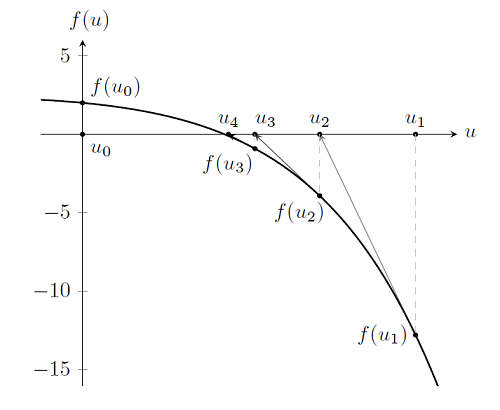
Таким чином, знаходження рішення нелінійної задачі по суті ідентично рішенням лінійної задачі, за винятком того, що тепер ми робимо багаторазові послідовні кроки по Ньютону-Рафсона, щоб отримати рішення. Насправді, ми можемо продовжувати робити ітерації і як завгодно близько підійти до вирішення, але в цьому немає необхідності. Як обговорювалося раніше, рано чи пізно ми досягнемо машинної точності представлення чисел на комп'ютері, так що завжди є практична межа наскільки можна наблизитися до вирішення. Давайте подивимося на результати декількох ітерацій:
i u_i | f (u_i) | | U_ {i-1} -u_i | | F (u_ {i-1}) - f (u_i) | 0 0.000 2.000 1 2.000 12.77 2.000 10.77 2 1.424 3.915 0.576 8.855 3 1.035 0.914 0.389 3.001 4 0.876 0.104 0.159 0.810 5 0.853 0.002 0.023 0.102 6 0.852 0.001 0.001 0.001
Ми бачимо, що після шести ітерацій різниця між двома послідовними значеннями f (u), і u, а також абсолютне значення f (u), зменшилася до 0.001-менш. Після шести ітерацій по Ньютону-Рафсона починаючи з u_0 = 0, рішення зійшлося з похибкою менш 0.001. При вирішенні нелінійних задач, ми застосовуємо цей алгоритм до тих пір, поки рішення не зійдеться з бажаною точністю. Є і другий критерій для завершення: вирішувач повинен зробити не більше певної кількості ітерацій. Незалежно від того, який критерій виконається першим - відносна похибка або число ітерацій - вирішувач зупинить процес. Також, необхідно пам'ятати про проблему чисельного масштабування, яку ми обговорювали в статті блогу про рішення лінійних статичних кінцево-елементних завдань. Критерій відносної похибки застосовується до масштабувати, а не до абсолютного вектору рішення.
Хоча показати це значно складніше, але алгоритм використовується для вирішення нелінійних задач, в разі коли u є вектором залишається тим же, що і для звичайної задачі. Однак, при вирішенні завдання з сотнями, тисячами або, навіть, з мільйонами ступенів свободи, бажано, щоб число ітерацій Ньютона-Рафсона було мінімально можливим. Нагадаємо, що нам необхідно вирішити задачу \ mathbf {u} _ {i + 1} = \ mathbf {u} _ {i} - [\ mathbf {f} '(\ mathbf {u} _ {i})] ^ { -1} \ mathbf {f} (\ mathbf {u} _ {i}), в якій обчислення зворотних похідних є найбільш ресурсозатратної процедурою. Щоб уникнути обчислень в області значень, свідомо не містять рішення, і мінімізувати число ітерацій Ньютона-Рафсона, в середовищі COMSOL використовується релаксаційний множник (коефіцієнт релаксації). Подивимося знову на початкову ітерацію Ньютона-Рафсона і її графік, і зауважимо, що для неї | \ mathbf {f} (\ mathbf {u} _ {i + 1}) |> | \ mathbf {f} (\ mathbf {u } _ {i}) | . Так що для цієї ітерації, ми робимо дуже великий крок. Коли це відбувається, COMSOL здійснює пошук вздовж інтервалу [\ mathbf {u} _ {i}, \ mathbf {u} _ {i + 1}] точки \ mathbf {u} _ {damped} = \ mathbf {u} _i + \ alpha (\ mathbf {u} _ {i + 1} - \ mathbf {u} _i) такий, що | \ mathbf {f (u} _ {damped}) | <| \ mathbf {f (u} _ {i }) | . Після чого, схема ітерацій Ньютона-Рафсона поновлюється з цієї точки.
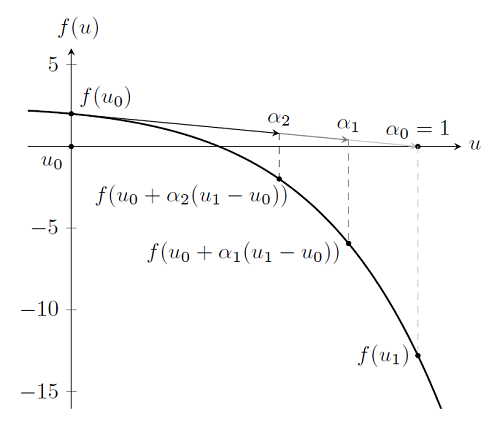
Параметр \ alpha відомий, як релаксаційний множник (коефіцієнт релаксації) і змінюється в інтервалі 0 <\ alpha \ le 1. При \ alpha \ rightarrow 0 ми говоримо, що релаксація зростає, а \ alpha = 1 означає, що завдання не срелаксірована. Цей метод досить привабливий, оскільки вимагає від середовища COMSOL тільки оцінки значення \ mathbf {f (u} _ {damped}), і обчислювальні витрати при цьому набагато нижче, ніж обчислення похідних \ mathbf {f '(u} _ {i}) і зворотних до них величин [\ mathbf {f} '(\ mathbf {u} _i)] ^ \ mathbf {-1}.
Важливо підкреслити, що параметр релаксації не має безпосередньої фізичної інтерпретації. Хоча метод дуже добре покращує збіжність, ніякого фізичного сенсу релаксаційний множник не несе. Більш того, хоча серед COMSOL дозволяє вручну регулювати релаксаційний множник, немає ніяких фізичних передумов або модельних уявлень, як і коли слід це робити. Обраний за замовчуванням алгоритм згладжування, дуже важко перевершити за допомогою ручного регулювання. Однак, існують інші методи, обумовлені, як правило, фізикою завдання, які добре працюють в тих випадках, коли релаксаційний метод Ньютона-Рафсона сходиться повільно або взагалі не сходиться.
Чому Рішення Нелінійної Завдання Можуть Не Зійтися
Нелінійні задачі по своїй суті складно вирішити, оскільки існує безліч причин, через які розглянута вище процедура вирішення може не зійтися. Хоча є багато причин, за якими the Newton-Raphson method can fail (метод Ньютона-Рафсона зазнає невдачі) , Ми обмежимося обговоренням наступних практичних випадків.
Випадок 1: Початкове Наближення Занадто Далеко від Рішення
Перш за все, розглянемо ту ж саму нелінійну задачу, але з іншого стартовою позицією, наприклад, u_0 = -2. З викладеного вище графіка нижче, якщо ми виберемо початкову точку в області u_0 \ le-1, метод Ньютона-Рафсона не зможе знайти рішення, так як похідні f (u) не дають точки перетину, що наближається до вирішення. Рішення не може бути знайдено зліва від u_0 = -1, так що ці початкові точки знаходяться поза радіусом збіжності методу Ньютона-Рафсона. Тобто через вибору початкового наближення метод Ньютона-Рафсона може не зійтися, навіть якщо рішення існує. Таким чином, на відміну від лінійного випадку, коли коректно поставлене завдання завжди буде вирішена, збіжність нелінійних моделей в сильному ступені залежить від вибору стартової позиції. Пізніше ми повернемося до питання, як найкращим способом вибрати початкове наближення.
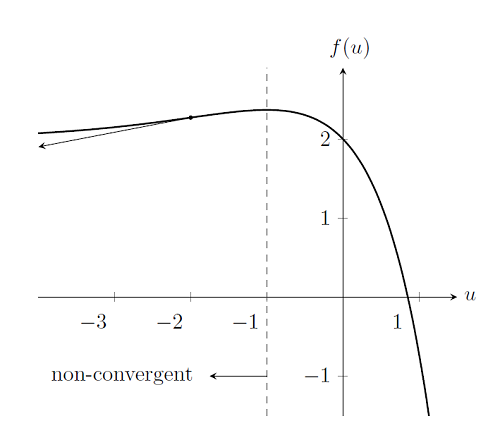
Випадок 2: Завдання Чи не має Рішення
Нелінійний вирішувач також зазнає невдачі, якщо завдання сама по собі не має рішення. Повернемося знову до задачі, розглянутої вище, але з жорсткістю пружини k (u) = \ exp (-u). Іншим словами, з розтягуванням жорсткість пружини зменшується. Якщо ми побудуємо графік f (u) для навантаження p = 2, ми побачимо, що рішення не існує. На жаль, алгоритм Ньютона-Рафсона не може визначити це самостійно; алгоритм просто буде намагатися знайти рішення і завершить свою роботу після заданого користувачем числа ітерацій.
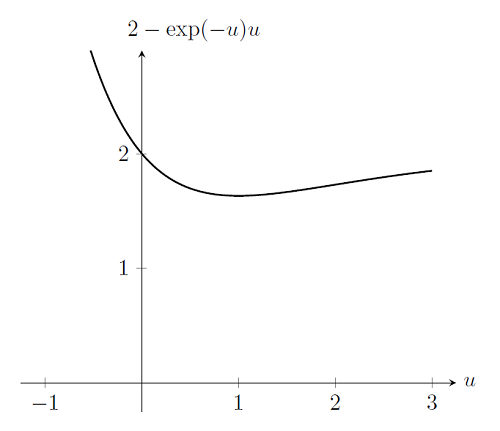
Випадок 3: Завдання Чи не Гладка і недіфференціруемого
Нарешті, розглянемо випадок, коли властивості матеріалу змінюються стрибкоподібним чином. Наприклад, розглянемо таку ж систему, як і перед цим, але з жорсткістю пружини, що приймає різні значення в різних діапазонах розтягувань, значення k = 0.5 для u \ le1.8, значення k = 1 для 1.8 <u <2.2, і k = 1.5 для u \ ge2.2. Якщо ми побудуємо графік f (u) для цього випадку, ми побачимо, що він недіфференціруем і розривів, а це порушує вимоги методу Ньютона-Рафсона. Легко переконатися безпосередньою перевіркою, що якщо стартова точка вибрана не в інтервалі 1.8 <u <2.2, то ітерації Ньютона-Рафсона будуть осциллировать за межами цього діапазону.
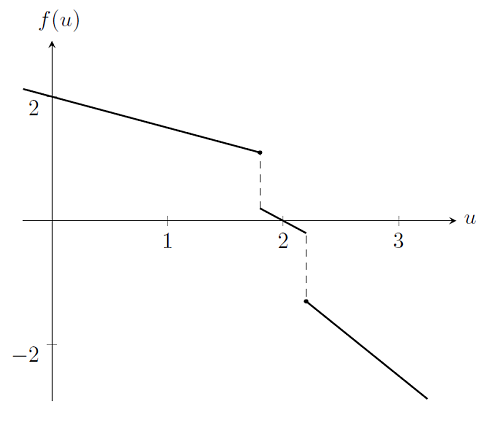
Підіб'ємо підсумки: ми описали релаксаційний метод Ньютона-Рафсона, який використовується для вирішення нелінійних кінцево-елементних завдань і обговорили критерії його збіжності. Ми вказали кілька причин, за якими цей метод може потерпіти невдачу при спробі знайти рішення, включаючи:
- Початкове наближення вибране дуже далеко від вирішення
- Поставлено завдання, яке не має рішення
- Завдання негладка і недіфференціруемого
Інтерпретація Log-файлу середовища COMSOL
Log-файл (системний журнал)
Найближчим часом ми обговоримо шляхи вирішення всіх цих питань, але перш, давайте подивимося на log-файл типовою нелінійної задачі кінцевих елементів. Подивіться на наведений нижче текст log-файлу (доповненого номерами рядків) геометричної нелінійної задачі з будівельної механіки:
1) Stationary Solver 1 in Solver 1 started at 10-Jul-2013 15:23:07. 2) Nonlinear solver 3) Number of degrees of freedom solved for: 2002. 4) Symmetric matrices found. 5) Scales for dependent variables: 6) Displacement field (Material) (mod1.u): 1 7) Iter ErrEst Damping Stepsize #Res #Jac #Sol 8) 1 6.1 0.1112155 7 3 1 3 9) 2 0.12 0.6051934 1.2 4 2 5 10) 3 0.045 1.0000000 0.18 5 3 7 11) 4 0.012 1.0000000 0.075 6 4 9 12) 5 0.0012 1.0000000 0.018 7 5 11 13) 6 1.6e-005 1.0000000 0.0015 8 6 13 14) Stationary Solver 1 in Solver 1: Solution time: 1 s 15) Physical memory: 849 MB 16) Virtual memory: 946 MB
роз'яснення
- Рядок 1 повідомляє про тип викликається решателя (обчислювача) і часу початку виконання завдання.
- Рядок 2 повідомляє, що викликане програмне забезпечення - це вирішувач нелінійних систем.
- Рядок 3 повідомляє про розмір завдання в термінах числа ступенів свободи.
- Рядок 4 повідомляє про тип матриці кінцевих елементів.
- Рядки 5-6 повідомляють про параметри масштабування. В даному випадку масштаб поля зсуву є 1 м, що є відповідним значенням для очікуваної величини рішення.
- Рядки 7-13 повідомляють, що шість ітерацій по Ньютону-Рафсона знадобилося для отримання сходиться рішення. Перший стовпець повідомляє про номер ітерації, а в другому наведені відомості про помилку, використовувані для визначення збіжності рішення. За замовчуванням, критерій збіжності дорівнює 0.001. Третя колонка показує, що для перших двох ітерацій використовувалася релаксація, але кроки 3-6 залишилися не срелаксірованнимі.
- Рядки 14-16 повідомляють про час отримання рішення та вимоги до обсягу пам'яті.
Тепер ви придбали розуміння того, як вирішуються нелінійні статичні завдання в середовищі COMSOL, а також знання, як інтерпретувати записи в log-файлі.



